Forward kinematics
Forward kinematics is the process of calculating the position and orientation of the end effector based on the given joint angles of the robot. It can be represented as a function f that takes the joint angles q as input and returns the position of the end effector x,y, and z as well as its orientation, and . For a simple one-joint robot, forward kinematics is straightforward and can be solved using trigonometry For robots with multiple joints, we can use the Denavit-Hartenberg convention, a systematic way of representing link transformations. This allows us to determine the end effector’s position and orientation in a 3D coordinate system.Inverse kinematics
Inverse kinematics is the process of determining the joint angles required to place the end effector at a desired position and orientation. It can be thought of as the inverse of forward kinematics: Inverse kinematics is essential for controlling the robot arm. It allows us to move the robot arm to a specific position and orientation in 3D space. It is a more complex process, as it involves solving a system of equations to determine the joint angles of the robot.- There may be multiple solutions (different joint configurations that reach the same end effector position).
- Some positions may be unreachable due to mechanical constraints.
- It often requires solving nonlinear equations, which may not have a direct solution.
Learn more
Learn more about Inverse Kinematics
Moving a robot
Since we control the actuators themselves, we can move the robot arm to a specific position by sending the joint angles to the actuators. This involves:- Reading the current joint angles from the motors.
- Solving the inverse kinematics problem iteratively to converge towards the desired joint angles.
- Sending these joint angles to the actuators to move the robot to the desired position.
- move/absolute: Move the robot arm to a specific position and orientation in 3D space.
- move/relative: Move the robot arm by a specific distance and rotation in 3D space.
Simulation
Simulations allow you to test movement models in virtual environments before applying them to a physical robot. They replicate real-world physics while remaining computationally efficient. Simulations are particularly useful for testing inverse kinematics, enabling safe and rapid iteration on motion planning before deploying on actual hardware.Learn more about simulation
Learn more about simulation
Note that no simulation prevents the need for real-world testing. Real world properties like materials, sensor noise, human interaction, and more can’t be fully replicated. Simulations themselves can have bugs or inaccuracies that affect results.Simulations are here to help you iterate faster, expand your mathematical toolkit, and reduce the risk of damaging hardware.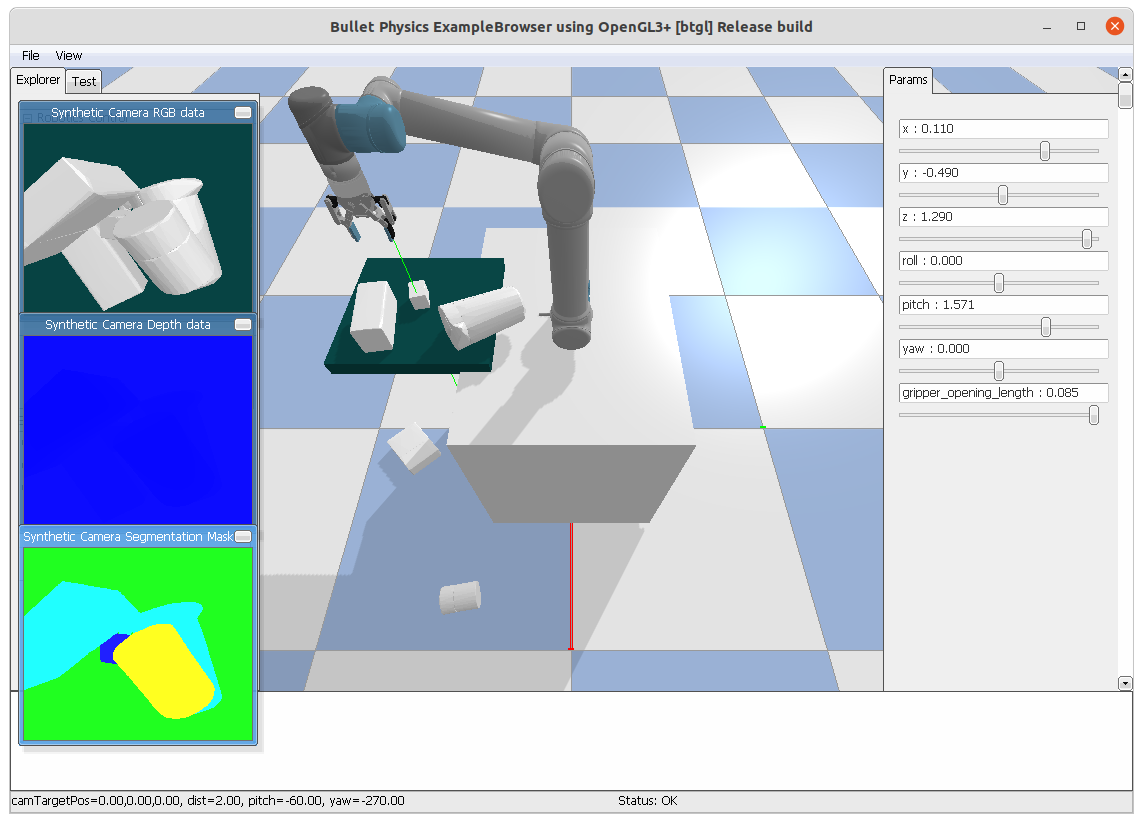

Trade-offs when choosing a simulation backend
- Simple tools are easy to use, but don’t offer the same level of realism. They are also less extensible.
- More realistic simulations need more computing power, which can be slow or expensive. They are usually more difficult to setup and can be overkill for simple tasks.
- Open-source options are flexible and community-driven, while proprietary ones might be more polished but costly and hardware-specific.
PyBullet
PyBullet is an open-source physics engine released in 2015. It is maintained by the community, but its maintenance status is currently inactive, with no new versions released in the past year.
Requirements
PyBullet uses URDF (Unified Robot Description Format) files to define robot structures. It’s lightweight and runs on most modern computers without specialized hardware.Features
PyBullet offers a balance between realism and computational efficiency, suitable for real-time simulations and educational purposes.Despite being old, Pybullet is easy to set up, with extensive documentation and community support.Pros: Easy to use, good community support, open source.Cons: Lack advanced features, inactive maintenance.
Learn more
Learn more about PyBullet
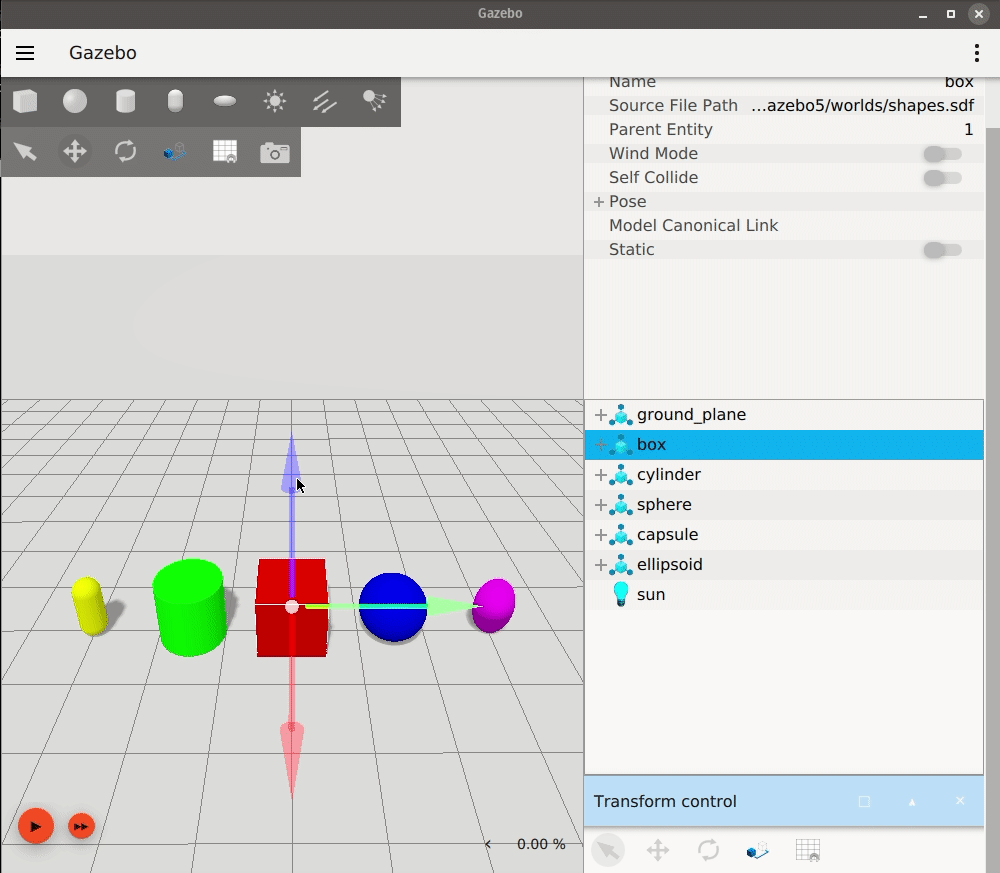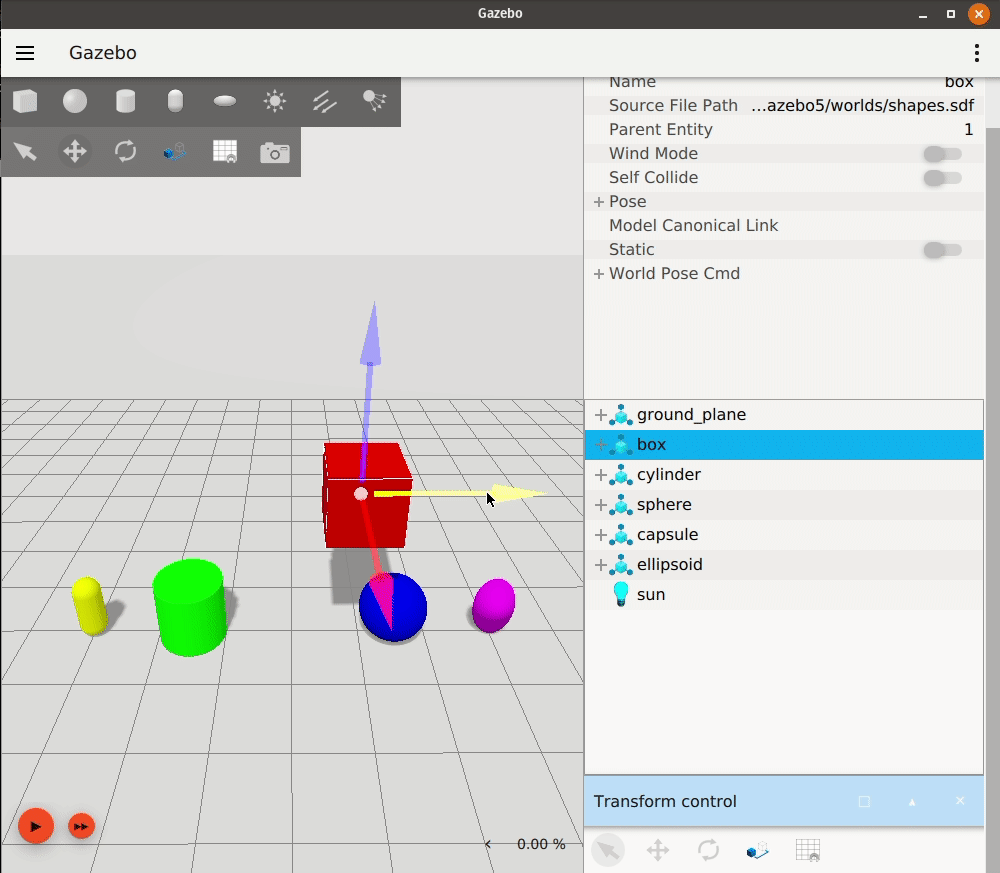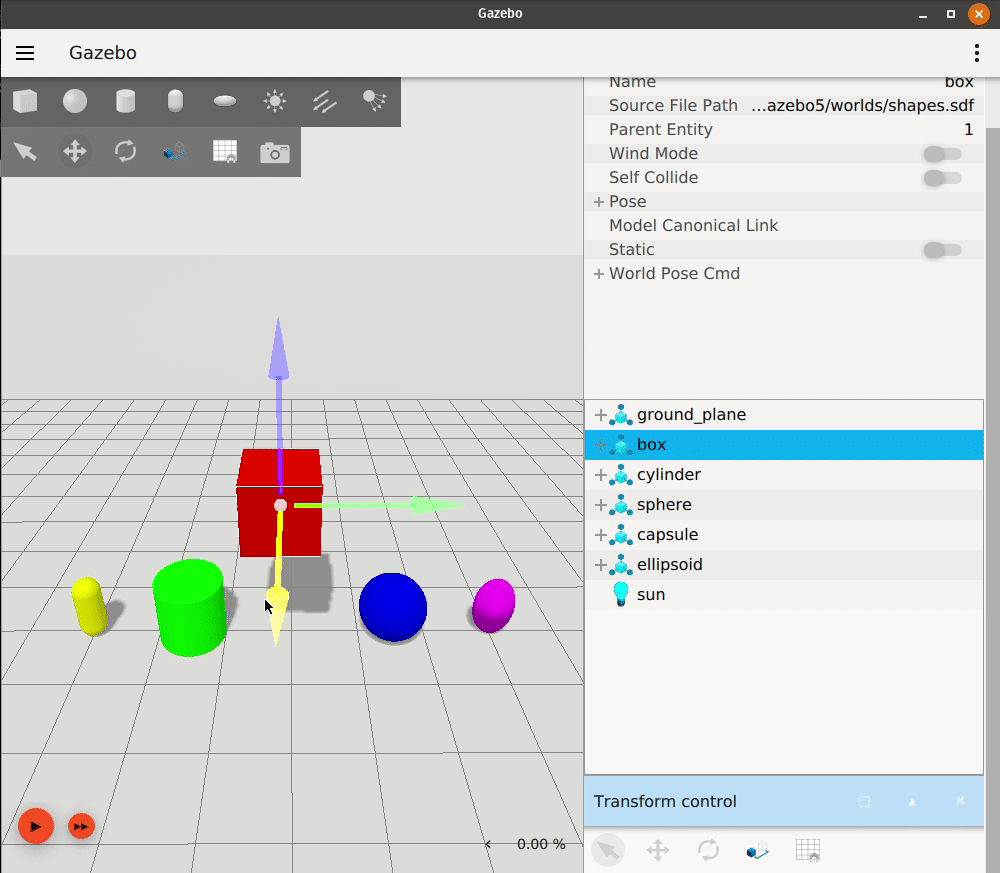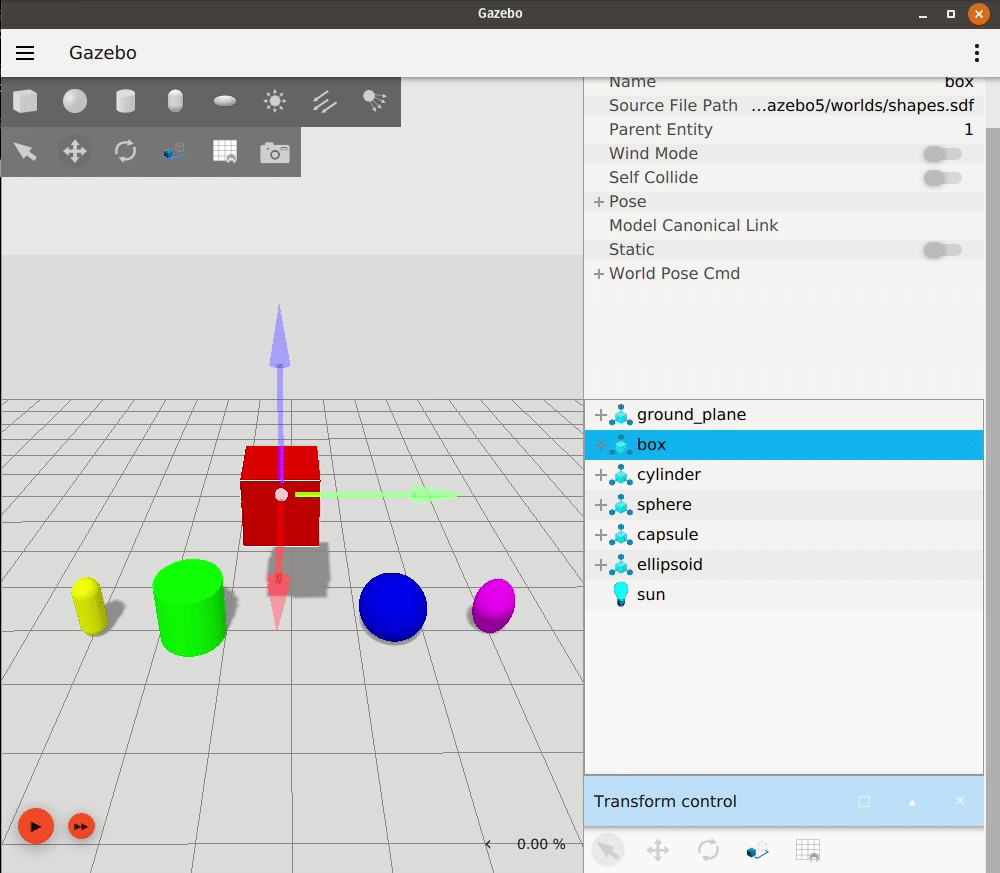
Gazebo
Gazebo is a well-established open-source robotics simulator that has been widely used in academia and industry since its initial release in 2004. It is maintained by Open Robotics and has a strong community of contributors.
Requirements
Gazebo uses SDF (Simulation Description Format) files to define robot models and environments. It supports a wide range of operating systems, including Linux, macOS, and Windows, and can run on standard hardware without the need for specialized equipment.Features
Gazebo provides a robust simulation environment with realistic physics, sensor models, and a variety of plugins for customization. It is particularly well-suited for testing robotic algorithms in complex environments.Gazebo is known for its ease of integration with ROS, making it a popular choice for robotics research and development.Pros: Strong community support, extensive documentation, ROS integration, open source.Cons: Can be resource-intensive, may require additional setup for advanced features.
Learn more
Learn more about Gazebo
MuJoCo
MuJoCo (Multi-Joint dynamics with Contact) is a powerful physics engine designed for simulating complex robotic systems. Initially released in 2012, it is now maintained by Google DeepMind and has become a staple in robotics research and development.
Requirements
Required Files: MuJoCo uses XML files, specifically the MJCF (MuJoCo XML) format, to define robot models and environments. This format allows for detailed specification of the physical properties and dynamics of the simulated entities.Hardware Requirements: MuJoCo is optimized for performance and can run efficiently on standard hardware. However, it really shines by running on GPUs and TPUs, making it suitable for data-intensive tasks like reinforcement learning.Features
MuJoCo is best for contact dynamics and complex interactions.Mujoco is straightforward to set up, with comprehensive docs. The recent open-source release has made it more accessible to researchers and developers.Pros: High fidelity, performance, flexibility, community, open source.Cons: complexity, hardware requirements, specialized use.
Learn more
Learn more about MuJoCo
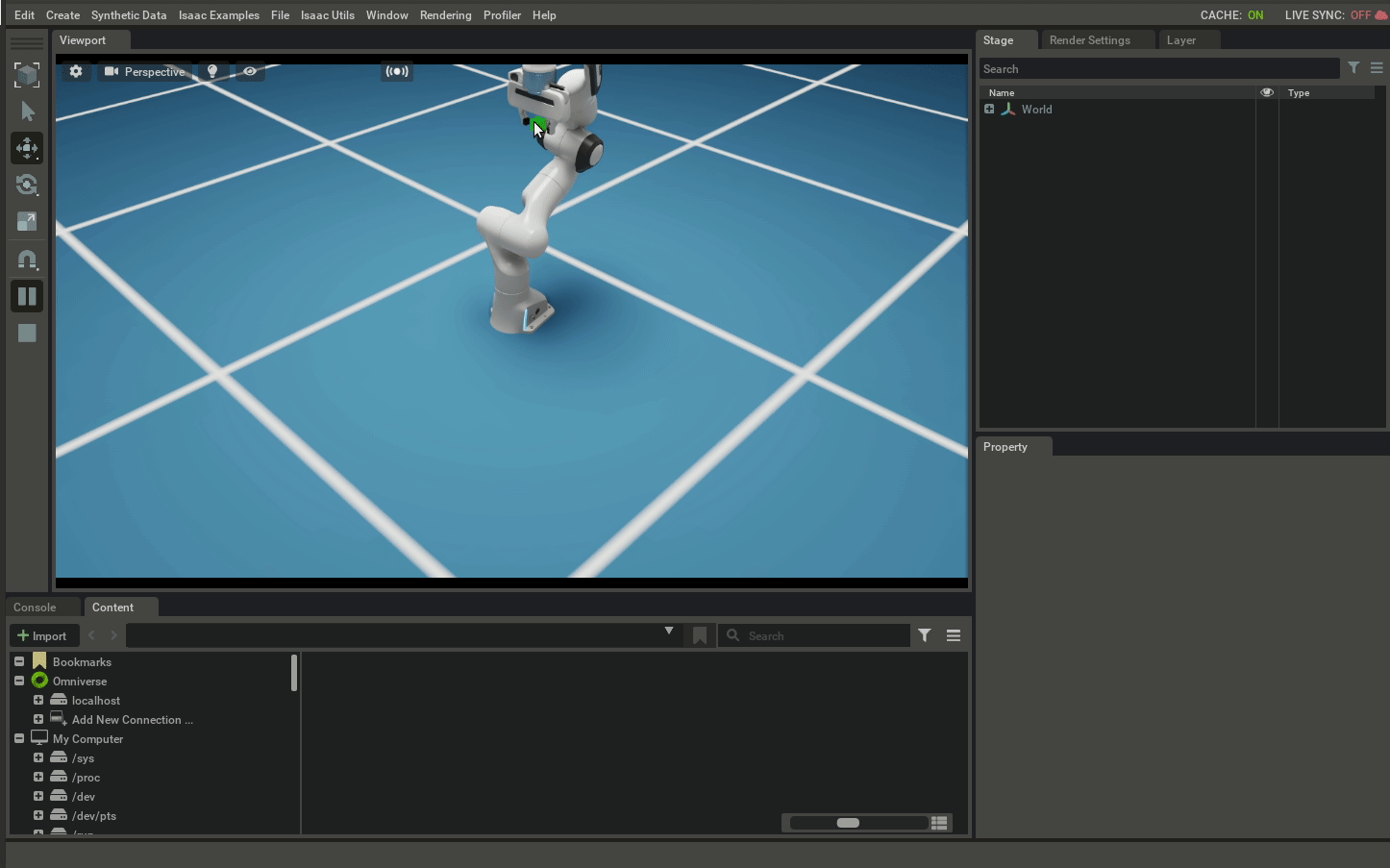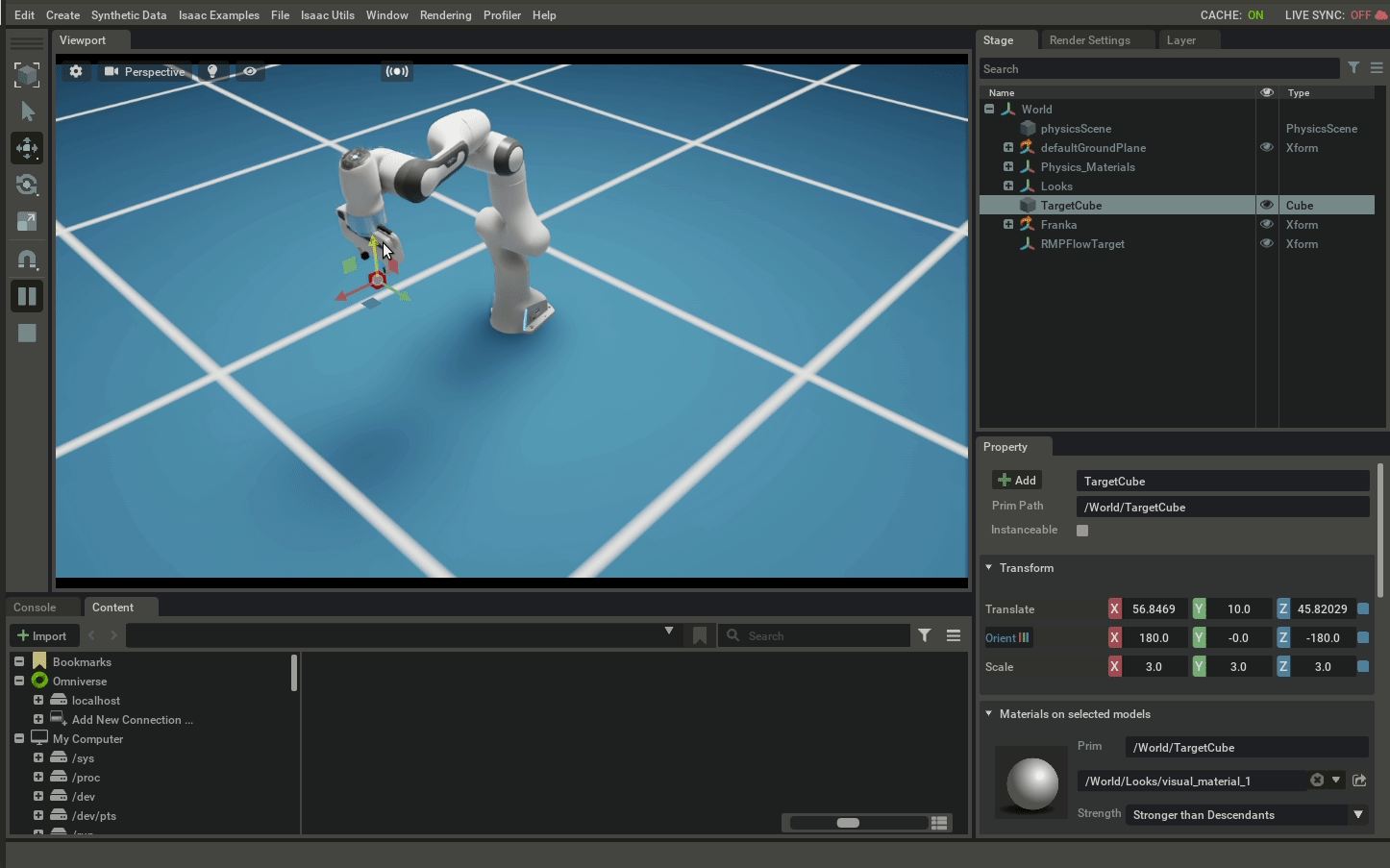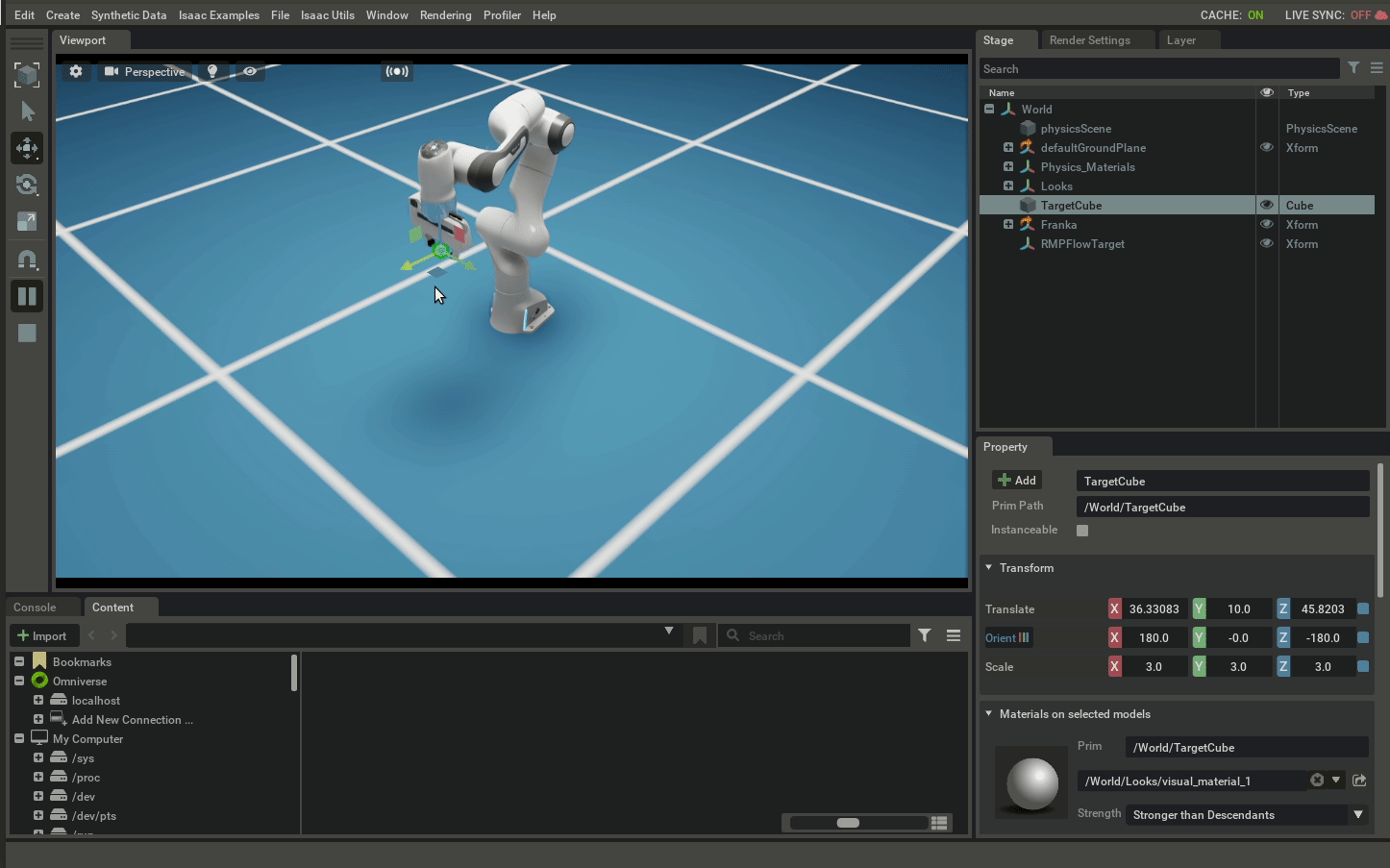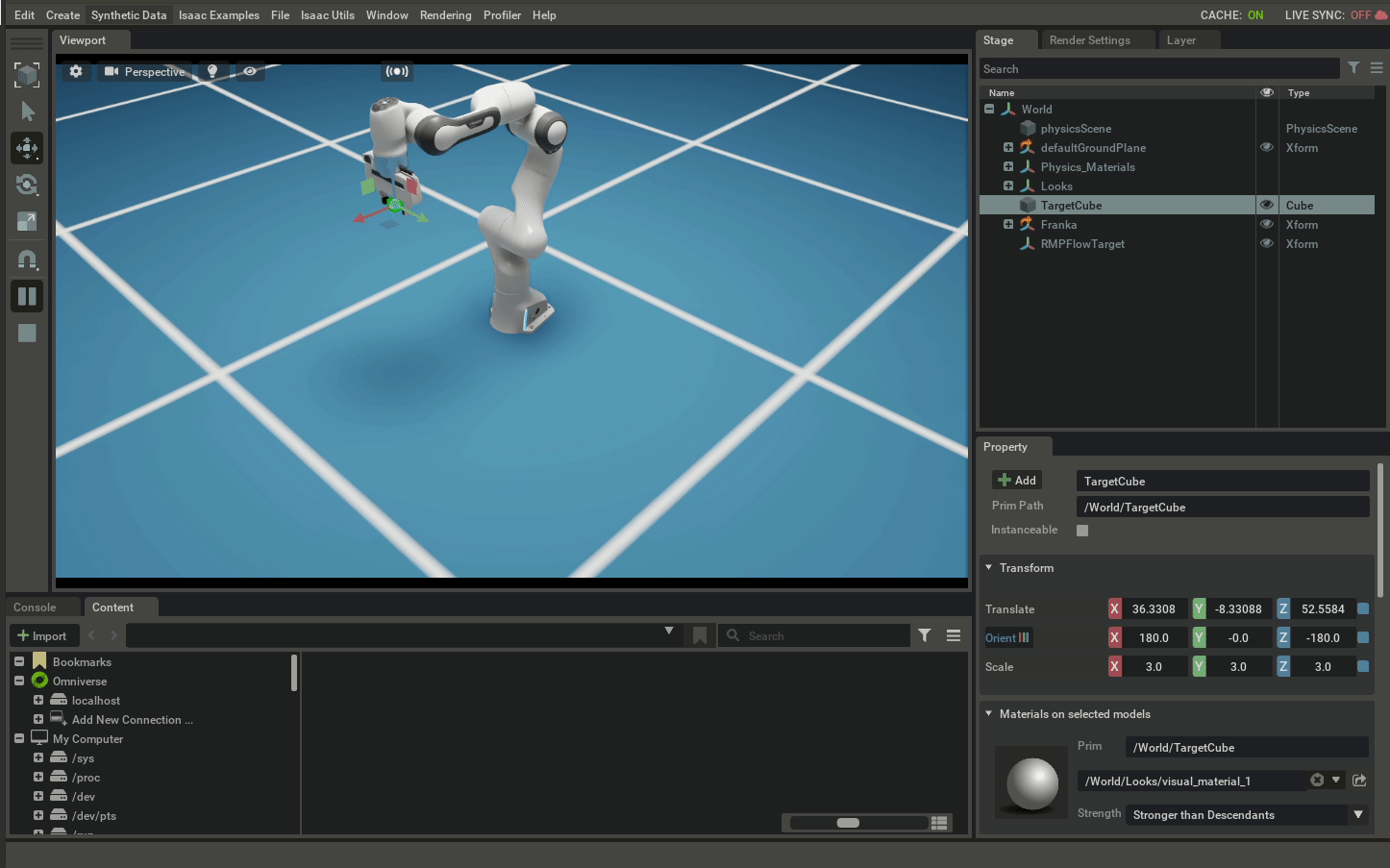
NVIDIA Isaac
Release and Maintenance: NVIDIA Isaac was released in 2018 and is maintained by NVIDIA, with the latest update in January 2025.
Requirements
Required Files: It uses USD (Universal Scene Description) files for defining environments and robots.Hardware Requirements: NVIDIA Isaac is optimized for NVIDIA GPUs, leveraging their power for high-performance simulations.Features
Nvidia Isaac provides a highly realistic simulation environment. It’s great for autonomous systems.Setting up NVIDIA Isaac can be complex, requiring specific hardware and software configurations.Pros: High realism, optimized for NVIDIA hardware, strong support for AI applications.Cons: Requires NVIDIA hardware, complex setup, closed source.
Learn more
Learn more about Nvidia Isaac Sim
Genesis
Genesis is a physics simulation platform designed for general-purpose robotics, embodied AI, and physical AI applications. Developed by a consortium of researchers, it was released in December 2024 and is maintained by the Genesis-Embodied-AI community.
Requirements
Genesis supports MJCF (.xml), URDF, and 3D model formats like .obj and .stl.The framework leverages GPU-accelerated parallel computation, making it highly efficient on modern GPUs. The current version is mostly compatible with Linux and Nvidia GPUs (CUDA), while support for other platforms is under development.Features
Genesis excels in simulating a wide range of physical phenomena, including rigid body dynamics, fluid mechanics, and soft robotics. It aims to let you train AI models and test robotic systems in complex environments.Genesis is designed to be user-friendly with a Pythonic interface, making it accessible to both beginners and experienced developers.Pros: high speed, wide range of physicals models, open source.Cons: requires powerful hardware, most features still under development.
Learn more
Learn more about Genesis